Several recent advances point the way toward real-time holographic television for telepresence, entertainment, and teleoperation. This article introduces the concepts and requirements for such systems, then presents the MIT Media Lab's work to make them practical and inexpensive.

by V. Michael Bove, Jr., and Daniel Smalley

THE NOTION of holographic television appeals to the popular imagination, figuring prominently in science-fiction movies and carrying enough cachet that the word "holographic" is often applied to systems that are not really holographic and sometimes not even 3-D, such as the "Pepper's ghost" illusions that have been used to re-create deceased celebrities onstage. Holographic TV also potentially provides some important technical advantages in that unlike two-view 3-D TV, it supplies in a consistent fashion all the visual cues to object shape and position, including focus ("accommodation") and motion parallax, increasing both viewer comfort for extended viewing and perceptual accuracy for precise tasks.

Research since the early 1960s has attempted to build true holographic television, but until very recently the prospect has seemed distant. The authors' group has for several years concentrated on developing holographic displays suitable for consumer applications, adding constraints of mass manufacturability, low cost, and compatibility with mass-market computational resources such as might be found in PCs or game consoles. A resurgence of consumer interest in 3-D displays, combined with several relevant technological developments, makes this an opportune time to explore re-imagining holographic displays as part of a home in the near future rather than in fictional spacecraft in the far-off future.

Before we consider technical requirements for building such a device, it is important to define precisely what a holographic display is, namely, a system that uses diffraction of light to reconstruct light wavefronts (or lightfields) associated with a desired visual scene. It is sometimes added that the diffraction pattern should be generated by interference between a coherent reference beam and coherent light reflected by a scene (or at least by a computational simulation of the interference), but for a display designer the physical characteristics of the necessary diffraction patterns are what matters.

Like all 3-D displays, holographic displays are bound by the behavior of light and – despite cinematic special effects to the contrary – cannot create images in free space or project them across a room. As shown in Fig. 1, from the point of view of the viewer, all parts of a reconstructed object must have the display behind them.

 

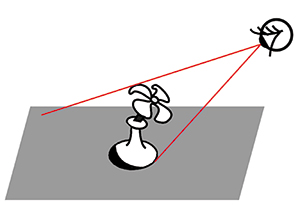
Fig. 1: From the eye's viewpoint, an object reconstructed by a hologram cannot extend past the edges of the display device.

Engineering Requirements

The realism of holographic displays and also the difficulty of building them can be traced to the physics of diffraction. A device is required – usually called a spatial light modulator (SLM) – that can change the amplitude (by varying its transmittance) and/or phase (by varying its index of refraction) of light waves passing through it with a fine enough pixel pattern that diffraction over a useful range of angles (which will be the viewing angle of the display) occurs. For typical display applications this means a pixel pitch of about the same size as the wavelength of visible light (or around half a micron).

Half-micron pixels may be smaller than the pixels in typical current microdisplays, but an even bigger challenge lies in the fact that physics constrains the pixel size to stay the same no matter the size of the display. Thus, such a display will need about 2 million pixels per scan line per meter of image width. It's not too difficult to make a tiny direct-view holographic image by illuminating a micro-display with a laser, but scaling this up to useful dimensions by tiling such displays together is a complicated proposition. Tiling of small devices nevertheless has been employed by several researchers to create larger images; if the device is fast enough, the tiling can also be done optically, where one device images in several positions sequentially.

A strategy that relaxes the need for such small pixels is to make a hologram with a smaller view angle (and thus larger pixel pitch in the SLM) and then use a steerable light source to direct the hologram where an eye tracker sees the viewer's pupils.¹ The pixel count and computational requirements reduce significantly if the hologram is made to have parallax only in the horizontal direction, as the vertical resolution then reduces to that of an ordinary television image, and the computation of each scan line can be carried out independently.

Diffraction

For clarity, the following diffraction discussion will be done in one dimension, with the extension to two dimensions straightforward (for a horizontal-parallax-only display, the process will happen in only one dimension). If a beam of monochromatic light enters a sinusoidal diffraction pattern, some will pass straight through (the undiffracted or zero-order beam) and beams will also come out at an angle to either side of the zero-order beam (the first-order diffracted beams). The resulting angle is a function of the ratio of the wavelength of the light to the spatial frequency of the pattern, while the amount of light that is diffracted is a function of the contrast of the pattern. Note here that the R/G/B illuminators will need to be monochromatic, as broadband illumination will diffract across a range of angles, leading to a blurry image.

Such grating patterns are created in optical holograms through interference, but the mathematics for synthesizing them from a three-dimensional model of a scene are tractable. This process can be carried out similarly for a computer-graphics model or for real imagery if sufficient information about the real scene can be captured.

If the spatial frequency of the sinusoid varies (a "chirped" grating), as in Fig. 2, and the pattern is illuminated with collimated light, beams at the higher-frequency end will be diffracted at more of an angle than those on the other end, giving the appearance that the light is coming from a point emitter.

 

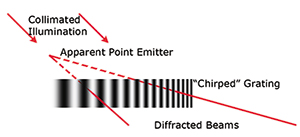
Fig. 2: Because a "chirped" diffraction pattern bends light by varying angles, when it is illuminated by collimated light, the result appears to be a point emitter at a particular (x,y,z) position. A scene can be built up by superposing about as many of these as there would be pixels in an ordinary image of similar apparent resolution.

 

Note that for this diffraction method to work, there must be a mechanism – which could be as simple as a barrier – for keeping the undiffracted and opposite-order light from reaching the viewer's eyes. It should be apparent that a 3-D scene could be built up by summing up chirped gratings corresponding to the points making up the scene. Such calculations are within the capabilities of modern PC or game-console graphics processors.²

Capture and Transmission

It is commonly assumed that the massive pixel count of display holograms makes transmitting real-time holographic television nearly impossible, and even if data compression could somehow reduce the data rate to something manageable, the requirement for coherent illumination of the scene and extremely short exposure times for moving imagery (because the scene has to be stationary to within a small fraction of a wavelength of light during the exposure) would still render the process impractical. Nevertheless, since the early days of holography, analysis and experiments have been carried out for coherent capture and real-time transmission.^3-5

Recent advances in two areas have opened up an alternative approach: non-holographic capture and calculation of the holographic interference pattern at the receiving end. Ordinary cameras have become small and inexpensive enough to permit building dense arrays of them, while small lightfield and rangefinding cameras have also become available. The outputs of each of these image acquisition strategies are more compact and easier to transmit than the holograms that would result from capturing the same scenes at the equivalent image resolutions, and current graphics processors and digital signal processors provide enough processing to do the necessary diffraction-pattern computation.

Thus, researchers have recently been able to demonstrate scene capture for holographic displays using a camera array,⁶ a lightfield camera,⁷ or a rangefinding camera.⁸ The authors' group at the MIT Media Lab has shown that the Microsoft Kinect can be used as the camera for a holographic television system, with Internet transmission of the resulting data and conversion to horizontal-parallax-only holograms at video rates on a standard PC with three graphics cards. Because the Kinect produces perspective views and the rendering algorithm needs an orthographic camera in the parallax direction, it is necessary to perform calibrated geometric correction as part of the process. Because a hologram captured with a single camera will have missing occluded regions visible from viewer positions far from that of the camera, for complex scenes or displays with large viewing angles it may be necessary to merge data from more than one rangefinding camera, requiring yet more calibration and correction. The resulting holograms have been demonstrated on both our display and a refreshable polymer display developed by the University of Arizona, College of Optical Sciences (Fig. 3).

 

Fig. 3: This hologram was generated from a Kinect camera and displayed on a refreshable photorefractive polymer display. Courtesy University of Arizona College of Optical Sciences.

 

Display Devices

Several generations of holographic video displays have been built at the MIT Media Lab since the groundbreaking Mark I display premiered by Stephen Benton and his students in 1989.⁹ Our current display project continues with the Scophony geometry used in its predecessors, where instead of a common light-modulator technology, the diffraction patterns are created by acoustic waves in a transparent material; as the pattern moves with the speed of sound, such systems need a mechanical scanner to provide a stationary hologram. Recent systems in our laboratory have employed our own lithium niobate guided-wave light modulator in place of the earlier bulk-wave acousto-optic modulators. These devices – similar to surface-acoustic-wave filters – can be fabricated with a modest two-mask process. In a guided-wave modulator, a waveguide is created just under the surface of the material, light is coupled into the waveguide, and diffraction is created by surface acoustic waves. One of our prototype modulators is shown in Fig. 4.

 

Fig. 4: In this photograph of a guided-wave light-modulator chip, laser light enters at left and diffracted light exits at right.

 

Our ultimate target is to fabricate devices with 480 or more independent waveguides, providing sufficient bandwidth to support large displays, but our immediate goal is to demonstrate a full-color horizontal-parallax-only 100-mm-wide proof-of-concept desktop display of SDTV resolution with a bill of materials in the hundreds of dollars.¹⁰

Figure 5 shows the basic architecture: the light output from the modulator passes through a lens, horizontal and vertical scanners (where the vertical scanner will eventually not be needed when the modulator has as many channels as the display has scan lines), a parabolic mirror, and a vertical diffuser. Because the diffracted light has a rotated polarization from the zero-order beam, removing the latter can be done with a polarizer. We first verified the operation of the display optics with a bulk-wave modulator (Fig. 6 shows a small full-color image) and are now using our guided-wave modulator. Full details of our experiments will be presented in an upcoming publication, but the optical design has proven to work, and Fig. 6 shows a full-color (though not 3-D) image from the display system.

 

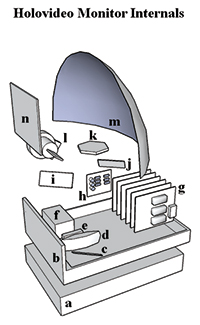
Fig. 5: This prototype display consists of a power supply (a), folded aluminum chassis (b), mirrors i and j (c), transform lens (d), light modulator (e), laser source (f), modulator driver cards with DVI-A inputs (g), phased-lock-loop control to drive the polygon (k), vertical scanner (l), parabolic reflector (m), and anisotropic diffuser (n). The vertical scanner will not be needed when the number of channels in the modulator increases to match the number of scan lines in the hologram.

 

Fig. 6: This single view of a small holographic stereogram test image (only 26 scan lines, not full screen) was displayed on the system shown in Fig. 5.

 

Holographic Television: A Work in Progress

A brief article such as this can just touch upon the basic principles; readers interested in exploring in depth the current state of display holography may want to look at a comprehensive recent technical overview by the author.¹¹ Much research and development remains to be done before holographic television is an everyday consumer product, but the practicality of real-time holographic viewing is being enabled by progress in a variety of technologies.

For a Q&A with V. Michael Bove about the processing demands of holographic television, see the October 2012 issue of Information Display.

Acknowledgments

Research described in this article has been supported by consortium funds at the MIT Media Lab and by a gift from Intel Corp. We also thank NVIDIA for providing graphics hardware used in this work.

References

¹R. Haussler, S. Reichelt, N. Leister, E. Zschau, R. Missbach, and S. Schwerdtner, "Large real-time holographic displays: From prototypes to a consumer product," Proc. SPIE Stereoscopic Displays and Applications XX 7237, 72370S (2009).

²Q. Y. J. Smithwick, J. Barabas, D. E. Smalley, and V. M. Bove, Jr., "Interactive holographic stereograms with accommodation cues," Proc. SPIE Practical Holography XXIV 7619, 761903 (2010).

³E. N. Leith, J. Upatnieks, B. P. Hildebrand, and K. Haines, "Requirements for a wavefront reconstruction facsimile system," J. Soc. Motion Picture Television Eng. 74, No. 10, 893–896 (Oct. 1965).

⁴L. H. Enloe, J. A. Murphy, and C. B. Rubinstein, "Hologram transmission via television," Bell Syst. Tech. J. 45, No. 2, 335–339 (Feb. 1966).

⁵R. J. Doyle and W. E. Glenn, "Remote real-time reconstruction of holograms using the Lumatron," Appl. Opt. 11, No. 5, 1261–1264 (1972).

⁶P-A. Blanche, A. Bablumian, R. Voorakaranam, C. Christenson, W. Lin, T. Gu, D. Flores, P. Wang, W.-Y. Hsieh, M. Kathaperumal, B. Rachwal, O. Siddiqui, J. Thomas, R. A. Norwood, M. Yamamoto, and N. Peyghambarian, "Holographic three-dimensional telepresence using large-area photorefractive polymer," Nature 468, No. 7320, 80–83 (2010).

⁷R. Oi, T. Mishina, K.Yamamoto, and M. Okai, "Real-time IP-hologram conversion hardware based on floating point DSPs," Proc. SPIE Practical Holography XXIII 7233, 723305 (2009).

⁸ J. Barabas, S. Jolly, D. E. Smalley, and V. M. Bove, Jr., "Diffraction specific coherent panoramagrams of real scenes," Proc. SPIE Practical Holography XXV 7957, 795702 (2011).

⁹P. St.-Hilaire, S. A. Benton, M. Lucente, M. L. Jepsen, J. Kollin, and H. Yoshikawa, "Electronic display system for computational holography," Proc. SPIE Practical Holography IV1212, 174–182 (1990).

¹⁰D. Smalley, Q. Smithwick, J. Barabas, V. M. Bove, Jr., S. Jolly, and C DellaSilva, "Holovideo for everyone: a low-cost holovideo monitor," Proc. 9th International Symposium on Display Holography (ISDH 2012) (2012).

¹¹V. M. Bove, Jr., "Display holography's digital second act," Proc. of the IEEE 100, No. 4, 918–928 (2012). •

 

---

V. Michael Bove, Jr., heads the Object-Based Media Group at the MIT Media Lab. He is co-author with the late Stephen Benton of the book Holographic Imaging (Wiley, 2008) and served as co-chair of the 2012 International Symposium on Display Holography. He can be reached at vmb@media.mit.edu. Daniel Smalley is a doctoral candidate in the Object-Based Media group at the MIT Media Lab. He can be reached at desmalley@gmail.com.