The Road Ahead to the Holodeck: Light-Field Imaging and Display
Light-field displays represent the 3-D of our future
by Jim Larimer
MODERN DISPLAYS can reconstruct 2-D and stereo-pair 3-D (s3D) imagery, but some important features of the natural visual environment are still missing; there
remains a visible gap between natural imagery and its reconstruction on even today’s most advanced display technologies. This gap can be closed as light-field technologies replace our current display systems. The light field is all of the information contained in light as it passes through a finite volume in space as we look in any direction from a vantage point within the volume. This article will describe the signals contained in the light field and captured by human vision that are missing with 2-D, s3D, and multi-view s3D displays. To understand what is missing, it is useful to understand the evolutionary context of biological vision.
A Brief History of Vision
Biological sensory systems evolved shortly after the Cambrian explosion, when predation became a part of life. Vision evolved so that creatures could find food and avoid being eaten. Vision plays a central role in cognition and our understanding of the world about us; it provides the basic information we use to orient in our immediate environment. Almost all ideas have images as correlates; a chair is a visual pattern, a tiger is a large cat. Even abstract concepts such as satisfaction can be imagined as a smile on a face. Visual cognition, understanding images, is not the mental equivalent of a photograph; our visual experience is more akin to Plato’s concept of Ideals and Forms. We see people, objects, and actions — not their images as projected onto our retinas.
Human vision is object oriented. We use information extracted from the light field and neural signal processing based upon learning and memory to understand the environment we sense from the images projected onto our retinas. The image formed on the retina is the raw data for vision; it is not a sufficient signal for image understanding by itself. To understand what we see, we change eye positions and focus to de-clutter or segment a scene into whole objects.
Not all of the information embedded in the light field is accessible to vision. Reconstructing information we cannot see is wasteful, just as leaving out
information we can see limits the veridicality of the virtual scene we experience on modern displays. Artists may wish to create non-veridical or distorted imagery in cinema and photography, but this is a choice the artist should make and not have made for them by the imaging technology.
Images exist because we have a chambered eye with an entrance pupil similar to a
pinhole camera or the camera obscura (Fig. 1). Understanding how our eyes extract useful information from the light field and the physics of light both began with the camera obscura. The camera obscura’s connection to sight was described by Mozi and Aristotle centuries ago and featured in da Vinci’s notes on light and imaging.1 The idea that light from a point on any surface can be considered as rays emanating in all directions external to the surface, a central idea in geometric optics, is based upon the pinhole camera. Evolution discovered the pinhole camera concept shortly after the Cambrian explosion almost 550
million years ago and a chambered complex eye like ours evolved over 500 million years ago.2
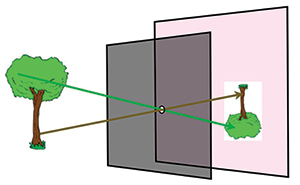
Fig. 1: A camera obscura or pinhole camera is shown in this illustration. The discovery of the pinhole camera gave rise to early ideas about the nature of light, vision, and optics. That light can be thought of as traveling in straight lines comes directly from this discovery.
Michael Faraday in 18463 was the first to describe light as a field similar to the field theory he developed for electricity and magnetism. Almost 100 years later, Gershun4 defined the light field as the uncountable infinity of points in three-space where each point can be characterized as a radiance function that depends upon
the location of the point in space and the radiance traversing through it in every direction (Fig. 2).
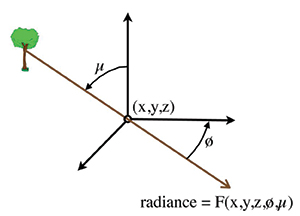
Fig. 2: An arbitrary point in space is shown with a ray that originated on the trunk of a tree passing through it in a direction relative to the point at azimuth and elevation angles ø and µ, respectively. The radiance in this direction through the point is F(x,y,z,ø,µ). This is Gershun’s definition of a point in the light field; Adelson and Bergen called this the 5-D plenoptic function.
Light traversing a point in the light field continues to move beyond the point until it encounters an impedance that can alter its course by reflection, refraction, or extinction. Every line passing through a point in the light field in terrestrial space will be terminated by two surfaces, one at each end. Every line segment defined this way contains two packets of information, each going in opposite directions. If the line segment is not very long and there is nothing to impede it, this
information is almost entirely redundant at every point on the line. The information is unique to the surfaces and light sources creating the packets, and this is the information biological vision has evolved to sample and use.
Adelson and Bergen5 called Gershun’s radiance function the 5-D plenoptic function, indicating that everything that is visible from a point in free space is contained in it. They described how our visual system extracts information from the light field to discover properties of objects and actions in our visual environment. The plenoptic function contains information about every unobstructed surface in the lines of sight to the point in space and by adding time, the 6-D plenoptic function, how these surfaces change. J. J. Gibson called the information we gather from the visual environment affordances6 because it informs behavior; for example, when to duck when something is looming towards us. Information that is not useful in affording an action is not extracted from the light field.
A pinhole camera forms an image based upon the plenoptic function at the location of the pinhole. The image formed by the camera is based upon at most half of the plenoptic function at this point and is limited by camera size, blur, and diffraction. The image formed depends only upon the direction from which a ray travels
through the pinhole. Images are therefore 2-D and flat. Information about depth in the visual field is missing in a single image. For example, image size is a function of both object size and the distance to the object from the entrance pupil of the camera. This information is ambiguous in a single image. Parallax produced by an object or camera motion or by the displacement of our two eyes and the resulting retinal image disparities provides the additional information required to disambiguate these two factors. Figure 3 illustrates how parallax is expressed in the relative location of the 2-D projections of objects on the projection plane of two cameras at different locations.
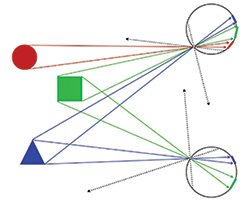
Fig. 3: A top-down plan view of three figures in the visual field of two spherical pinhole cameras is shown in this drawing. The two cameras view the visual field from two different locations, and this results in changes in the relative locations and extents of the images of these
objects on the projection surfaces. These differences are due to parallax. At the lower location, the red object is totally obscured by the green object,
and there is no image of it visible on the projection surface. The relative change in location and rate of change as either objects or the camera move through space provides information about the range and size of objects in the visual field. To extract this information requires signal processing in the visual system.
Our visual system has evolved neural mechanisms that use parallax to estimate the distance to objects and the closing rates of looming objects. These estimates are based upon data extracted from the light field sampled over a period of several milliseconds. Object recognition and identification, linear and aerial perspective, occlusion, familiarity, and other features of the imagery projected onto our retinas over time are all used by the visual system to augment our image understanding of the location, size, range, surface relief, etc., of objects in the visual field.
Real pinhole cameras have entrance apertures or pupils that are larger than a point. The image formed by a pinhole camera is the sum of many points or plenoptic
functions located within the entrance aperture. As the size of the aperture is enlarged to let in more light, the resulting image becomes blurry. The resolution limit of a real pinhole camera is limited by diffraction as the aperture size is reduced and by blur as it is enlarged. There is a trade-off between image intensity and image clarity.
Evolution has overcome this tradeoff by evolving a lens located near the pupil that allows us to focus the light traversing the pupil, sharpening the images of some objects but not all objects in the field of view simultaneously. The depth of fielda of the image is determined by the diameter of the entrance pupil and the eye’s focus. Focus is determined by where we place our attention in the visual field. Blur is a cue used to estimate the size and the relative depth to objects.7
In and Out of Focus
The information in the light field passing through the pupil becomes more or less accessible to visual cognition depending upon the eye’s focus. Focusing superimposes all of the rays passing through the pupil from many plenoptic functions that originated at single points on the surface of objects that are in focus onto single points in the image projected onto the retina. Every in-focus point in the visual field will project to one point on the retina. Rays originating on out-of-focus points are spread over the retina in circles of blur whose size depend upon focus and pupil diameter. Figure 4 illustrates focus for a schematic eye showing four bundles of rays that originated from each of the ends of two arrows. The blue arrow is in focus and the green arrow is not.
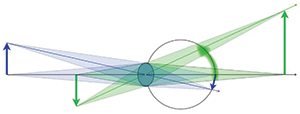
Fig. 4: This diagram shows a schematic eye focused on the blue arrow. The transparent blue and green bundles are the rays from the end points of both arrows that form images of the end points on the retina. The blue arrow’s image is sharp on the retina and the bundles converge to a point on the retina. The green arrow would come to focus on a projection plane behind the retina. Rays emanating from the green arrow end points are spread or blurred over a wide area of the retina. When an out-of-focus object occludes an in-focus object, the blur reduces the image contrast of parts of the in-focus object.
Focusing the image on the projection surface aggregates information from all the rays passing through the pupil. When the information in these rays is correlated, i.e., originated from the same point on an in-focus surface, the aggregate signal is strengthened. When the rays projected onto retinal locations come from several different surface points, and are therefore uncorrelated, information is mixed together and blurred, reducing the signal strength and image contrast. The information captured from the light field is not lost, but to see it we must focus on different surfaces.
Image-capture and reconstruction in traditional 2-D and s3D imaging systems do not support refocusing, and the only parallax information available in s3D is fixed by the location of the two cameras. When viewing natural scenes we move our eyes and translate and rotate our heads to obtain more parallax information from the light field. We can re-focus our eyes to rearrange and sort the bundles of rays coming from all the points that traverse our pupils.
The signal for focusing is missing with traditional image technology as is a great deal of the parallax information, but our visual system evolved to use this information. The result can be annoying and uncomfortable. For example, when viewing a large displayed image the viewer might attempt to view an object on the screen that is out-of-focus or she may move her head to see around something in the scene. No effort on the viewer’s part can bring an out-of-focus object in a displayed image into focus or allow her to see behind an occlusion.
A 2-D video sequence during which the camera moves, or in which objects are moving in the scene, can evoke the perception of depth in a scene, but as soon as the motion stops, these motion-parallax-driven cues, along with the sense of depth, are lost. The inability to see around occlusions and the fixed image focus in standard 2-D
and s3D imagery are the missing and/or inaccessible light field data.
Light-Field Cameras
Cameras that can retain the perceptually relevant information in the light field have been developed. The idea for this camera has many sources: Lippmann or Ives,8 and, more recently, Adelson and Wang9 and Ng et al.10 The company Lytro recently introduced a light-field camera into consumer markets and a commercial version of a light-field camera is available from Raytrix.11 (For more about these cameras, see the article, “Communication through the Light Field: An Essay,” in this issue.) Understanding how these cameras capture the light field reveals what is required to build a true light-field display capable of reconstructing parallax information appropriate for any head position and that supports attention-driven focusing.
A plenoptic camera is similar to an ordinary camera or to the eye in its basic design. To illustrate the principles of operation of a plenoptic camera, a spherical camera similar in geometry to the eye will be used. We will call the entrance aperture of the plenoptic camera the pupil and the projection surface where images are formed will be called the retina. The eye’s lens is located very close to the eye’s pupil and we will imply the same geometry for this plenoptic camera, although that is not a requirement. A plenoptic camera has an array of tiny pinhole camerasb located where the retina would be located in a real eye. These tiny cameras capture images of the rays passing through the pupil. Every pinhole camera has its own unique entrance aperture, its pinhole, located at uniformly spaced positions within this array of tiny cameras replacing the
retina in our illustration. Two of these pinhole cameras are illustrated very much enlarged in Fig. 5; all of the other pinhole cameras are too small to be seen in this illustration.
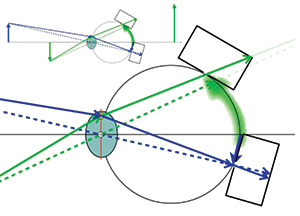
Fig. 5: Ray tracings for two rays originating at the tip of the green arrow and two rays originating at the tip of the blue arrow are followed as they come to focus at different depths in the upper small illustration. The blue arrow is in focus on the retina whereas the green arrow comes to focus behind the arrow. The enlarged illustration traces the rays as they are captured by or miss the apertures in the case of the green dashed ray of two pinhole cameras located on the retina.
Every tiny camera captures a slightly different image depending upon its location in the array. Where rays from points in the 3-D object space enter the plenoptic camera depends upon the location of these points in the visual field, the 3-D object space. Where rays traversing locations in the pupil of the plenoptic camera are
projected onto the pinholes in the tiny camera array depends on the plenoptic camera’s focus. A plenoptic camera does not require a lens that can change its focal length to make sharp images of any point in the visual field. It can bring any point into focus by rearranging the data captured by the array
of tiny pinhole cameras. This requires some computation in addition to the array of tiny pinhole cameras.
Two rays from separate points in the 3-D object space entering the plenoptic camera at the same location in the pupil will generally be imaged to separate pinhole cameras. Two rays entering the plenoptic camera from the same point in 3-D object space will only be projected to the same pinhole in the tiny camera array if their
point of origin is in focus. This is illustrated in Fig. 5.
Figure 5 traces four rays as they traverse the pupil and are projected onto the pinhole camera array. One ray from each of the blue and green arrow tips passes through the center of the pupil; these rays are shown as dashed lines in the figure. A second ray from each arrow’s tip passes through the same peripheral location in the pupil; these rays are represented as solid lines.
The blue arrow is in focus, so the lens projects both the dashed and solid blue rays to the same pinhole camera location in the tiny camera array. The two rays are traced as they pass through the pinhole at this location and are projected onto the back surface of this tiny camera. The locations of the rays on the pinhole camera’s back surface are correlated with the entrance pupil locations of the rays, which are correlated with the location of the point in the 3-D object space at
which both of these rays originated. This is the directional information that is lost in ordinary cameras. Most or even all of the rays projected onto this pinhole will have originated at the same point on the blue arrow’s tip. The image projected on the back surface of this pinhole camera records each ray’s location in the pupil.
The dashed and solid green lines tracing the path of rays from the green arrow tip are projected to different locations on the pinhole array because this arrow is not in focus. Different pinhole cameras will record the directional information contained in these two rays. The plenoptic camera nonetheless captures all of the directional information contained in these rays, so no directional information is lost.
In summary, rays originating at points in focus in the scene will be captured by a single pinhole camera in the array and rays originating from out-of-focus points will be captured by different pinhole cameras. Capturing the directional information is the key to capturing the light field in a small region in free space, i.e., where the plenoptic camera’s entrance aperture is located.
Figure 6 illustrates what happens in a plenoptic camera when two points in 3-D object space are located along the same direction from the eye and one point is nearer to the eye than the other. This is illustrated with points on the base of the two arrows illustrated in Fig. 5. The green arrow is out of focus and its base occludes some of the rays from a point on the base of the in-focus blue arrow. The entire bundle of rays originating at a point on the base of the green arrow will be projected onto the pinhole camera array of the plenoptic camera as a small circle of blur, i.e., different rays going to different locations on the retina. In this illustration only the non-occluded half of the bundle of rays that originates at a point at the base of the blue arrow passes through the plenoptic camera’s pupil. The base of the green arrow occludes the other half of this bundle of rays. Therefore, only one-half of the blue rays in this bundle are sharply focused on the pinhole camera at this retinal location. These rays from the blue arrow are imaged on the pinhole camera’s back surface, covering half of it. In the middle of the image formed by this pinhole camera is a small portion of the green rays from the out-of-focus green arrow base. The image formed by this pinhole camera from rays originating at these two points is shown as an inset in Fig. 6.
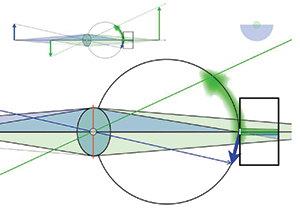
Fig. 6: The small upper-left illustration traces two bundles of rays originating from the base of two arrows as they are traced to their conjugate points on the images formed by the lens. A pinhole camera placed at the location where the blue bundle of rays comes to focus captures an image of the bundle as it passes through the lens. The bundle of rays from the green arrow would form a circle of blur at this image depth, so the pinhole camera captures a fraction of the rays in this bundle as a small spot on the pinhole camera’s projection surface. The image of the rays from both bundles as captured by the pinhole camera is shown as the insert in the upper right of the illustration.
This is an example of how blur can mix rays from different objects together, reducing the contrast of portions of sharp images formed on the retina when two
objects at different depths are near the same direction on a line of sight from the eye. This is an example of the how the parallax information contained in two distinct plenoptic functions whose xyz locations in 3-D space are separated by less than the diameter of the pupil is lost in ordinary image capture by a camera or the
eye. A plenoptic camera retains this information in the pattern of images formed on the array of tiny pinhole cameras replacing the retina.
These off-pupil-center rays from all of the points in 3-D object space are the signal that our eyes use to focus. Without direct access to these signals we cannot focus. These rays contain some information regarding what is behind an occluding object, but nothing compared to the information we obtain by moving our heads
or from the separation between our two eyes. In a light-field camera instead of the eye, the entrance aperture can be very large. As this aperture gets bigger the camera can look farther behind occluding objects. A light-field or plenoptic display must reconstruct this information and it must perform this reconstruction for every head location and orientation within the viewing space where the eyes might be located. This is the inverse of the sampling operation performed by the plenoptic camera, with the caveat that the samples must also include a wide variety of locations within the visual field corresponding to any pair of eye locations from which a display user might view the plenoptic or light-field display.
There are fundamental resolution limits to be considered now that the operational principles of light-field imaging have been described. Sampling is a quantization and a windowing problem. The volume of space to be reconstructed and the volume of real space from which it can be viewed determine the number of rays that must be reconstructed for a light-field display to operate. The larger these spaces become, the more rays will be required. This is a standard clipping or windowing issue; how much of the space can be clipped away before the volume is too small to be useful? That is a task-dependent question.
The same spatial and temporal resolution requirements apply to a light-field display that apply to ordinary displays. At half-a-meter viewing distance, a 100-dpi display produces about 15 line-pairs per degree of visual angle, adequate for many display tasks at this viewing distance. For a handheld display that will be viewed closer to the eye, 200 dpi or more is appropriate. Temporal-resolution requirements are the same as in current displays. Avoiding or controlling temporal artifacts such as flicker, judder, motion blur, and a recently documented temporal artifact in s3D imaging12 must be considered to determine the frame rates required for any specific task.
Figure 7 depicts a light-field display in top-down plan view. The front surface of the display is the light-blue side of the rectangle with the blue fill. The blue fill represents the light-field volume that can be reconstructed on this display. This volume can be viewed only from locations within the yellow fill. Two individuals, each with a single eye, are looking at the red dot. It must appear at locations 1 and 2 on the front surface of the display. For the eye on the right, the green dot is also visible on the screen at the same location the red dot is visible to the left eye, i.e., location 1. This illustrates the requirement that a light-field display must be capable of reconstructing directional views to objects that appear at different front-screen locations depending upon where the viewer is located. A light-field display reconstructs parallax information for any head location or rotation relative to the display screen within the viewing window.
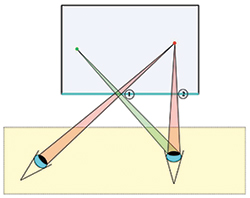
Fig. 7: A hypothetical light-field display is illustrated in a top-down plan view. The blue edge at the bottom of the blue rectangle represents the front surface of the display. The light-blue area in the rectangle is the reconstructed light-field volume and the yellow rectangle represents the viewing window in which viewers can correctly view the space. The screen surface at the point labeled 1 must be able to send rays corresponding to the green dot in the viewed volume to the eye on the right while simultaneously sending rays corresponding to the red dot to the eye on the left. This is the task of the plenoptic display.
The light-green and light-pink pyramids represent the bundles of rays from each dot that are traversing the pupils of these two eyes. Multiple rays within these bundles are required if observers are to be able to arbitrarily focus on any object within the reconstructed light-field volume. This would be possible if the front surface of the display was an array of micro-projectors that could project independent rays at each location of the front surface of the display towards every location where the viewer’s eyes might be located. A video display produced by Zebra Imaging based upon this architecture will be the described at the SID Display Week Technical Conference in May in Vancouver.13
To focus the eye at any arbitrary depth within the reconstructed volume, more than a single ray from every surface point in the virtual volume must be included in the bundles of rays passing through the viewer’s pupil for every possible eye location within the viewing space. This is the data that is captured by the plenoptic camera. The reconstruction of this data is slightly more complicated than its capture because the eye’s optics must be considered again. It is these bundles of rays traversing the display viewer’s pupil that allow the eye to focus at any arbitrary depth within this volume. The Zebra Imaging light-field video display described in Ref. 13 provides parallax and unique s3D information for every viewer location, but lacks sufficient rays to support arbitrary focusing.
In the camera discussion, the number of rays captured at any pinhole camera location in the plenoptic camera corresponded to the number of independent locations or pixels on the sensor on the back surfaces of the pinhole camera. This resolution determines the depth of field in which the data can be rearranged through image processing to bring an object into focus or the number of stereo pairs for s3D viewing that can be reconstructed from the captured data.
How many rays are needed at each location, or correspondingly, how many rays from every surface point in the virtual space must pass through the eye’s pupil at any arbitrary location in the viewing space? The answer is the angular ray resolution requirement for a light-field display. This requirement is related to the ability of the human eye to see a change in blur and this is related to pupil diameter and the point-spread function of the eye.
Akeley et al.14 constructed a prototype display for a single eye position that allows viewers to focus arbitrarily within a finite volume, but only from a fixed-eye location and only with some important cheats. Occlusion is not supported in this quasi-light field display. To understand how they did this, imagine looking at a point on a plane in space that is perpendicular to your line of sight. How far in front or behind this plane would another point have to be placed before you noticed it was blurry? This distance defines planes of just perceptible blur and measured in diopters, they are equally far apart.
Suppose a viewer is focused on a point on a plane and a second point is either one blur distance in front or behind it. Suppose the number of rays being reconstructed from the second point is finite and that some number of them, say n, traverse the viewer’s pupil. Because this point is out of focus, these n rays will be imaged within the blur circle of the eye for real points on a surface this far removed from an in-focus point in the field of view. If those n rays form n perceptually distinct points, then the viewer could discern that these are different from a real blur circle. The real blur area would not be completely covered in this case, so it would be noticeably different from real blur. If, on the other hand, there is no noticeable difference between the n points created by the n rays from this light-field reconstruction and the blur created by real objects, then the observer would have no way of knowing that this reconstruction is different from a real light field created by a real object. This is the key to figuring out how many rays are required. At this point in time, this number has not been determined in the lab. Nor is it known at what number of rays a sufficient signal for focus is produced. It could be that we could focus with fewer or more points than are required to match all possible blur circles. Figure 8 illustrates the case where the number of rays from an out-of-focus object is inadequate and the individual rays would be visible to the observer and therefore inadequate to reconstruct the light field.
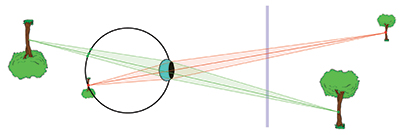
Fig. 8: The vertical blue line represents the surface of a plenoptic display and the two trees depicted to the right of it are in the virtual space of the display. The pink and green bundles represent the trajectories of all the rays from two points on the trunks of these two virtual trees that might traverse the observer’s pupil. The screen must reconstruct an adequate number of these rays. Suppose from each virtual tree trunk location only three rays reconstructed on the screen traverse the pupil. For the in focus pink bundle these three rays are superimposed on the retina, but for the out of focus green bundle these rays are projected onto the retina with large gaps between the rays. The observer would detect the sparse reconstruction as a series of distinct dots instead of a blur circle, so this display would not adequately reconstruct the light field. More rays would be required to traverse the observer’s pupil from every screen location.
The lab apparatus built by Akeley et al. employed three planes spaced between 0.5 and 1 diopter apart. With this apparatus, a volume roughly 25 cm deep close to the eye was reconstructed. Their cheats allowed them to trick the eye into focusing at any depth within this volume by approximating the blur circles and by avoiding scenes where this scheme would produce conflicting signals.
Light-Field Displays
Many display architectures for light-field displays are possible. Schowengerdt et al.15 described a head-mounted light-field display at Display Week 2010 based upon a novel fiber-optic projector. Most recently, Fattal et. al., described a light-field display based upon diffractive optics and light guiding, where images are created by turning on and off light sources. The spatial, temporal, tone-scale, and angular resolution of these future light-field displays will depend upon individual application requirements. The additional angular resolution requirement will determine the amount of arbitrary user-unique focusing a specific display device will support. We can expect these parameters to be traded off like any other engineering trade-off, to suit the application requirements. No display, including the light-field display, needs to exactly match nature; it only needs to be veridical enough for an observer to not see or care about the difference.
The challenges for light-field displays will involve developing display architectures that can be manufactured reliably and inexpensively, developing signal processing and addressing bandwidth schemes that are consistent with the capabilities of electronic components, and discovering the engineering trade-offs most appropriate for each application. Once these hardware challenges are overcome, only a light-field communications infrastructure that includes capture, transmission, and reconstruction will be the remaining barriers to realizing light-field imaging. It was only 20 years ago that some people doubted that the CRT could ever be completely replaced as the backbone of video technology; it would be difficult to speculate on how rapidly light-field technology will roll out.
References
1J. Needham, Science and Civilization in China: Volume 4, Physics and Physical Technology, Part 1, Physics (Caves Books, Ltd., Taipei, 1986); Aristotle, Problems, Book XV; J. P. Richter, ed., The Notebooks of Leonardo da Vinci (Dover, New York, 1970).
2M. F. Land and D-E. Nilsson, Animal Eyes (Oxford University Press, ISBN 0-19-850968-5, 2001).
3M. Faraday, “Thoughts on Ray Vibrations,” Philosophical Magazine, S.3, Vol. XXVIII, N188 (May 1846).
4A. Gershun, “The Light Field” (Moscow, 1936). Translated by P. Moon and G. Timoshenko in Journal of Mathematics and Physics, Vol. XVIII, pp. 51–151 (MIT Press, Cambridge, MA, 1939).
5E. H. Adelson and J. R. Bergen, “The plenoptic function and the elements of early vision,” in Computation Models of Visual Processing, M. Landy and J. A. Movshon, eds. (MIT Press, Cambridge, MA, 1991), pp. 3–20.
6J. J. Gibson, The Senses Considered as Perceptual Systems (Houghton Mifflin, Boston, MA, 1955), ISBN 0-313-23961-4; J. J. Gibson, “The Theory of Affordances,” in R. Shaw & J. Bransford, eds., Perceiving, Acting, and Knowing: Toward an Ecological Psychology (Lawrence Erlbaum, Hillsdale, NJ, 1977), pp. 67–82.
7R. T. Held, E. A. Cooper, and M. S. Banks, “Blur and Disparity Are Complementary Cues to Depth,” Current Biology 22, 1–6 (2012); R. T. Held, E. A. Cooper, J. F. O’Brien, and M. S. Banks, “Using Blur to Affect Perceived Distance and Size,” ACM Transactions on Graphics 29, 1–16 (2010).
8G. Lippmann, “Epreuves reversible donnant la sensation du relief,” J. de Physique 7, 821–825 (1908); H. E., Ives, “Parallax Panoramagrams Made Possible with a Large Diameter Lens,” JOSA 20, 332–342 (1930).
9T. Adelson and J. Y. A. Wang, “Single lens stereo with a plenoptic camera,” IEEE Transactions on Pattern Analysis and Machine Intelligence 14, 2 (Feb), 99–106 (1992).
10R. Ng, M. Levoy, M. Brédif, G. Duval, M. Horowitz, and P. Hanrahan, Light Field Photography with a Hand-held Plenoptic Camera, Stanford Tech Report CTSR 2005-02.
11www.lytro.com and www.raytrix.de
12D. M. Hoffman, V. I. Karasev, and M. S. Banks, “Temporal Presentation Protocols in Stereoscopic Displays: Flicker Visibility,
Perceived Motion, and Perceived Depth, J. Soc. Info. Display 19, 255–281 (2011).
13M. Klug, T. Burnett, A. Fancello, A. Heath, K. Gardner, S. O’Connell, and C. A. Newswanger, “Scalable, Collaborative, Interactive Light-Field Display System” (to be published in the 2013 SID Symposium Digest of Technical Papers).
14K. Akeley, S. J. Watt, A. R. Girshick, and M. S. Banks, “A Stereo Display Prototype with Multiple Focal Distances,” ACM Transactions on Graphics 23, I804–813 (2004).; K. Akeley, “Achieving Near-Correct Focus Cues Using Multiple Image Planes, Dissertation submitted to the Department of Electrical Engineering and the Committee on Graduate Studies of Stanford University (2004).
15B. T. Schowengerdt, M. Murari, and E. J. Seibel, “Volumetric Display Using Scanned Fiber Array,” SID Symposium Digest Tech. Paper 41, 653-656 (2010).
16D. Fattal, Z. Peng, T. Tran, S. Vo, M. Fiorentino, J. Brug, and R. G. Beausoleil, “A Multi-Directional Backlight for a Wide-Angle, Glasses-Free Three-Dimensional Display,” Nature 495, 348–351 (2013). •
aDepth of field is the distance between the nearest and farthest objects in the visual field that are sufficiently sharp to be characterized as in-focus.
bThe tiny camera array does not necessarily have to be made of pinhole cameras; these tiny cameras could have lenses. The principles of operation of the plenoptic camera would be the same in either case.
Jim Larimer is a retired NASA scientist and long-time member of the SID. He consults on human-factors issues related to imaging. He can be reached at jim@imagemetrics.com. Note: Jim Bergen and David Hoffman made helpful suggestions to improve an early draft of this article. All remaining confusions and errors are mine, not theirs.