Blue Phases for LCDs Based on Isotropic-to-Anisotropic Transitions
Novel LCD materials with fast response times and no requirement for alignment by rubbing have recently been developed. The polymer-stabilized blue phases, which exhibit electric-field-induced transitions from an optically isotropic state to an anisotropic one, boost the response speed of electro-optic switching without surface treatment.
by Hirotsugu Kikuchi
LIQUID-CRYSTAL DISPLAYS (LCDs) are very popular and are considered mainstream for flat-panel displays (FPDs). Behind the recent prominence of LCDs lies a significant improvement in moving-image display technology, which has long been considered a significant disadvantage of LCDs as opposed to self-luminous displays such as plasma displays. However, although improvements have been realized through the use of liquid crystals with improved response times and with driving techniques such as overdrive and black-frame insertion, a complete solution has not been achieved. Because these complex driving schemes increase cost, there is a strong thrust toward improving the fundamental response times of liquid crystals.
An innovative liquid-crystal material whose speed is more than an order of magnitude greater than that of conventional LCD materials has successfully been developed; furthermore, alignment processes such as rubbing are not necessary with this material. In this article, the basic characteristics of innovative liquid-crystal materials, their display mechanisms, the present state of the art, and the challenges that remain will be discussed.
The Blue Phase
There are many liquid-crystal phases: among them, the nematic, smectic, and chiral-nematic phases are well-known. Essentially, nematic materials are the most widely adopted (we must use the word "essentially" because chiral-nematic liquid crystals are used in the TN mode to be exact). Promising materials for higher-speed applications include ferroelectric, anti-ferroelectric, and banana-shaped liquid crystals; all of them are smectic. The blue phase is another liquid-crystal phase, different from both the nematic and smectic phases. It is seen only in a very narrow temperature range between the chiral-nematic phase, which is characterized by a relatively short helix pitch, and the isotropic phase. The blue phase has very singular characteristics 1-3:
• It exists in a narrow temperature range (typically about 1°C).
• It is optically isotropic in the voltage-off state.
• It is optically active because it has Bragg reflections.
• There are three types, refered to as blue phase 1, blue phase 2, and blue phase 3 in order from the low-temperature side.
• Blue phases 1, 2, and 3 have body-centered cubic, simple cubic, and isotropic symmetries, respectively.
• The lattice constants of the unit cells of blue phases 1 and 2 are typically a few hundred nanometers, and the phases show Bragg diffraction in the UV–visible range. The term "blue phase" originates from the color of diffracted light; many actually appear bluish, but some do not.
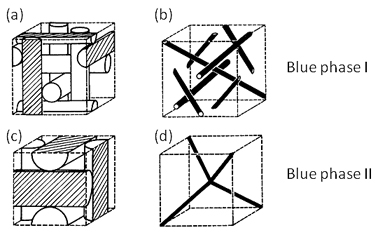
Fig. 1: This schematic illustration of the blue-phase structure shows blue-phase 1 [(a) and( b)] and blue-phase 2 [(c) and (d]).
The blue phase has a long history, beginning from when liquid crystals were first discovered in 1888, but the inner nature of this specific phase became clear only in the 1980s. The blue phase had long been left unnoticed, probably because of the very narrow temperature range in which it exists and its optically isotropic nature, which is unique in liquid crystals. In the 1980s, it became known that the phenomenon of frustration, a very new concept in liquid-crystal science, serves to bring forth the blue phase. Researchers then began to show more interest in and seek a better understanding of this phase. An important and basic characteristic of the blue phase is its complex 3-D hierarchical structure, which will be discussed in the following section.
Blue-Phase Structure
Both experimentally and theoretically, it is known that a blue phase forms a giant cubic crystal whose lattice constant is on the order of optical wavelengths (several hundred nanometers). A simple calculation indicates that there are 107 molecules in a giant, cubic unit lattice. The biggest problem encountered in the study of the blue phase in the 1980s was to determine how such a great number of molecules are aligned in the lattice. Figure 1 shows the currently accepted model of the blue-phase structure.
Figures 1(a) – 1(d) show the structures of blue phases 1 and 2, respectively.1,2 Blue phase 1 has a body-centered cubic lattice structure and blue-phase 2 has a simple cubic lattice structure. The cylinders in Figs. 1(a) and 1(c) show double-twist cylinders, and the bold black lines in Figs. 1(b) and 1(d) show disclinations (defect lines). In each double-twist cylinder, molecules are radially twisted through 90°. The molecule is parallel to the cylinder axis at the cylinder center and is tilted by 45° against the cylinder axis at the outer radial periphery. In other words, the molecule is twisted from –45° to +45° from end to end. This corresponds to a quarter pitch (a 360° twist is one pitch). The diameter of a double-twist cylinder is typically about 100 nm, and a simple calculation shows that approximately 200 molecules with the molecular diameter of 0.5 nm are mildly twisted. The lattice constant for blue-phase 1 corresponds to one pitch of helix, and the lattice constant for blue-phase 2 corresponds to a half-pitch of helix. We generally see a very small mismatch in pitch length with that of the lower-temperature chiral-nematic phase. Peculiar to soft matter, a complex hierarchical structure is formed in a self-organized manner as a result of repetitively twisted molecular alignment. It is interesting to see that behind this structure is frustration between space topologies that smoothly connects the doubly twisted geometry and 3-D space. (Articles in referenced textbooks explain more about frustration.1-3) A disclination (a type of defect line), which stems from frustration, is formed as if it runs through the corner where the three double-twist cylinders orthogonally come close to one another. The symmetry in the disclination geometry is body-centered cubic in blue-phase 1 and simple cubic in blue-phase 2. It is estimated that the diameter of a disclination core is about 10 nm, and the inner molecular alignment is as disorderly as it is in the isotropic phase. Although details are not yet available, blue-phase 3 has also been identified; it is presumed that its structure is amorphous and that there is only doubly twisted short-range order.
Due to the very large periodic structure as discussed above, the blue phase exhibits Bragg diffraction in the UV–visible range. Blue-phase 1 exhibits diffraction from the planes (110), (200), (211), etc., from the long-wavelength side, and blue-phase 2 shows diffraction from the planes (100), (110), etc. The following equation holds:
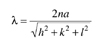
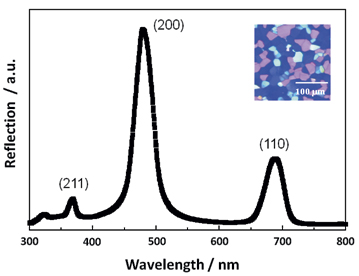
Fig. 2: The reflection spectra of blue-phase 1.
Here, λ, n, and a are the incident wavelength, refractive index, and lattice constant, respectively, and h, k, and l are Miller's indices. For blue-phase 1, h, k, and l are even numbers. Figure 2 shows an example of the reflection spectrum of blue-phase 1; there are several reflection peaks, which is not the case for the chiral-nematic phase. Typically, the diffraction from the (110) and (200) planes in blue-phase 1 and from the (100) plane of blue-phase 2 are in the blue region, which is the origin of the term "blue phase."
For display applications, all diffraction wavelengths should be shifted out of the visible range. There are two methods to do so: changing the lattice constant and controlling the alignment. Here, an example is presented where the chiral-dopant concentration is controlled to decrease the lattice constant. Figure 3 shows the chiral-dopant concentration dependence of the diffraction peak from the (110) plane for blue-phase 1.
As the chiral-dopant concentration increases, the lattice constant decreases, and the diffraction peak shifts to the low-wavelength side. Because the diffracted light from the (110) plane has the longest wavelength, shifting it to the UV range eliminates the colored background in the visible range; the color is black under crossed polarizers.
Polymer-Stabilized Blue Phase
It has long been believed that the temperature range of the blue phase is too narrow. Today, however, many attempts have been made to solve this problem.
In 1993, Kitzerow et al. formed a blue phase with polymerizable liquid-crystal monomers; the monomers were polymerized in the blue phase, which immobilized the molecules, thus preserving the blue-phase structure in the solid resin.4 In this type of material, although the characteristics of the blue-phase structure had been preserved, the dynamics of the liquid crystal had been lost because all of the molecules had been polymerized.
Then, in 2002, the authors reported that the temperature range of a blue phase could be increased to over 60°C by forming a small amount (7–8 wt.%) of polymers in the blue phase; the material was called the "polymer-stabilized blue phase" (Fig. 4).5
The molecular dynamics are not lost in the polymer-stabilized blue phase, and, moreover, the electro-optical response is very fast. It is believed that the polymers in the blue phase condense around disclinations, and the blue phase is stabilized when the disclinations are thermally stabilized.
In 2005, Yoshizawa et al. synthesized T-shaped liquid-crystal molecules and achieved a temperature range of 13°C for the blue phase.6 These authors suggested that the biaxial nature played an important role.
In 2005, Coles et al. reported a temperature range as large as 44°C in the cooling process for a dimeric liquid crystal with strong flexoelectricity.7 They suggested that flexo-electricity stabilizes disclinations. It is interesting, from an application standpoint, that in this system, the diffraction wavelength of the blue-phase lattice varies reversibly with the electric field.
As discussed above, technologies have recently been advanced in important ways to solve the problem of the narrow temperature range of the blue phase, and we now strongly believe in the prospective future of the blue phase.
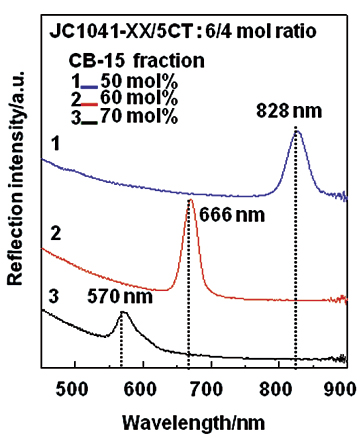
Fig. 3: Shown is the dependence of chiral-dopant concentration in blue-phase 1 on the (110) reflection peak.
Electro-Optical Effects and Driving Techniques
Because the blue phase is optically isotropic, a dark field under crossed polarizers occurs if the diffraction due to the lattice structure is shifted out of the visible range. The index ellipsoid is then an ideal sphere. Initially, therefore, there is no viewing-angle dependence originating from the liquid-crystal structure. However, when an electric field is applied, anisotropy or birefringence appears with the direction of the electric field as the optical axis. The index ellipsoid becomes an elongated ellipsoid stretched in the direction of the electric field if the dielectric anisotropy of the host crystal is positive. Conversely, we obtain a flattened ellipsoid contracted in the direction of the electric field if the dielectric anisotropy of the host crystal is negative. Therefore, the blue phase exhibits electric-field-induced birefringence of the type from which we can switch between optical isotropy and anisotropy, i.e., from zero to finite birefringence with the application of an electric field. Induced birefringence is proportional to the square of the electric field at small fields. This type of electro-optical effect is significantly different from that in conventional liquid crystals, where the initial state is anisotropic and the optical axis changes with the electric field (see Fig. 5).
Electric-field-induced birefringence also exists in the polymer-stabilized blue phase and the polymer-stabilized isotropic liquid crystal, called the pseudo-isotropic phase. In the pure blue phase, i.e., free from polymers, we see the local reorientation of molecules, lattice distortion, and phase transition as the electric field increases. But in the polymer-stabilized blue phase, the latter two effects are suppressed, and we only see the high-speed local reorientation of molecules.
To exploit electric-field-induced birefringence in display applications, we simply control the polarization of the incident light through the optical retardation produced by the induced birefringence, similar to the mode of retardation control used for IPS. As shown in Fig. 6, if a simple comb-shaped IPS electrode is used for the drive, the optical axis of the induced birefringence is parallel to the electric field, and the optical axes lie mainly in a plane perpendicular to the comb.
Superiority to Competing Technologies
The optically compensated bend (OCB) and ferroelectric-liquid-crystal (FLC) modes are known modes used for fast-response LCDs. The OCB mode is characterized by bow-shaped liquid-crystal orientation, called the bend alignment, and can achieve switching times of less than 5 msec because of the small alignment change between the on- and off-states. The OCB-mode displays initially suffered from large transition times for switching from the initial splay mode to the bend-alignment mode, but the problem has been solved and the technology is now much closer to seeing practical use. The FLC mode is characterized by a switching speed of less than 1 msec and shows great potential. The key to its high speed lies in the tilt direction change caused by the inversion of spontaneous polarization in an FLC (such as chiral smectic C). But hurdles that remain include alignment handling and the stability of the alignment structure. Recently, a group led by Prof. Takezoe from the Tokyo Institute of Technology proposed a new high-speed LCD using the SmA-like phase of a banana-shaped liquid crystal, which achieves a fast switching time of about 100 μsec.
The polymer-stabilized blue phase and the polymer-stabilized isotropic phase also show unprecedented promise because of their overall merits: fast switching times (<1 msec), no need for alignment processing, and a wide temperature range.
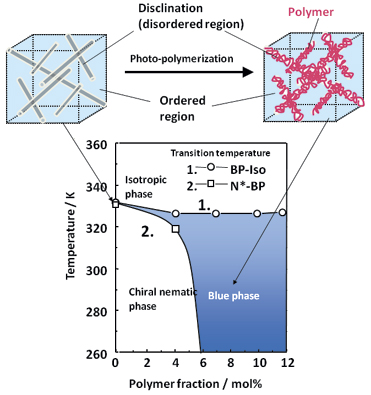
Fig. 4: This schematic illustrates polymer-stabilized blue-phase 1 (PSBP1) and the aggregation state of polymers in PSBP1.
Current State of the Art and Remaining Challenges
The most significant possible problem with the polymer-stabilized blue and isotropic phases is the need for large driving voltages. The short correlation length in orientational order is the source of both the fast switching speed and the large driving voltage. In fact, several tens of volts are required across an electrode distance of 10 μm. Although by decreasing the electrode distance the driving voltage could be reduced, there would be a limit to the fabrication of small electrodes. The driving voltage of the polymer-stabilized blue phase depends on the dielectric aniso-tropy, birefringence, and elastic modulus of the host liquid crystal,10 the fraction and structure of polymers, and the helical pitch (chiral-dopant concentration). Although there could be some other parameters, it is not easy to reduce the driving voltage to levels on the order of those used by conventional nematic liquid crystals merely through improvements in the material. It is very likely that improved electrode structures will be required for practical applications.
Residual birefringence will become a serious problem if the dielectric anisotropy and the birefringence of the host liquid crystal become greater. This is a phenomenon in which birefringence does not disappear after the electric field is applied and then removed. By improving the uniformity of the polymer network in the cell, the problem is partly, but not wholly, solved.
The light shield is an important factor in controlling display contrast. In the polymer-stabilized blue and isotropic phases, short-wavelength light is apt to leak through because, while diffraction and scattering occur mainly in the UV range, the longer wavelength tail is still in the visible range. This problem would not occur if the lattice constant and the correlation length of short-distance ordering are sufficiently small, but there is a trade-off with driving voltage.
Target Applications
Successful use of high-speed liquid crystals such as polymer-stabilized blue and isotropic phases in practice would lead to major improvements in LCDs. High-frequency driving would greatly improve the moving-image performance and reduce the effects of residual images.
Furthermore, higher speeds can lead to much lower power consumption. The field-sequential LCD, which is considered a promising future display system, drives the optical sources for the three primary colors in synchronism with the switching of the liquid crystals, thus realizing a full-color display without color filters. As a result, power consumption is considerably reduced simply because color filters, which absorb 70% of the backlight, are eliminated. No less important is the fact that higher-resolution images will be obtained because, by eliminating the color filters for RGB colors, the number of pixels per unit area could be increased threefold, and, further, the wiring could be simplified. A prerequisite for field-sequential LCDs is a more than threefold increase in speed, which cannot be realized easily with nematic crystals. Polymer-stabilized blue and isotropic phases allow for improvements of more than one order of magnitude over nematic crystals and are best suited to field-sequential-LCD systems.
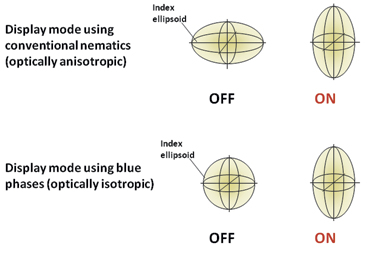
Fig. 5: Comparison of the electro-optic modes of conventional nematic LC and the blue phase.
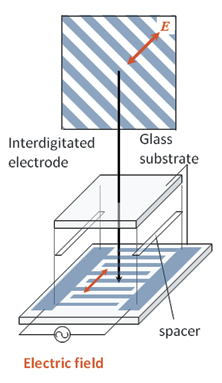
Fig. 6: Shown is a simple IPS electrode structure. Switching between the dark and bright states can be accomplished by switching the electric field on and off; the usual configuration is that the polarizing axes of the two (before and after) polarizers are orthogonal and the two axes are set 45° off the direction of the comb.8,9
Summary
Although both polymer-stabilized blue and isotropic phases have truly excellent characteristics, they have innate problems stemming from their structures and driving mechanisms, not to mention many as-yet unidentified factors. In the FPD industry, with excellent products and heated competition, the barrier for introducing an entirely new display mode could be considerably high. Under the circumstances, we greatly applaud the achievement of Samsung in demonstrating a blue-phase prototype panel. Although there is room for improvement in image quality, realizing a blue-phase TFT-LCD of significant size is an impressive step. In order to put the technology to practical use, an essential requirement will be cooperation among the various organizations in terms of the responsibility for materials, fabrication processes, device design, drive circuits, etc.
Acknowledgments
This work was partly supported by the Japan Science and Technology Agency and the Japan Society for the Promotion of Science. The authors thank Chisso Co., Ltd., for providing the nematic mixture.
References
1D. C. Wright and N. D. Mermin, Rev. Modern Phys. 61, 385 (1989).
2P. P. Crooker, Chirality in Liquid Crystals, H. S. Kitzerow and C. Bahr (eds.) (Springer-Verlag, New York, 2001).
3H. Kikuchi, Structure and Bonding (Springer-Verlag, Berlin Heidelberg, 2008), Vol. 128, pp. 99-117.
4H. S. Kitzerow, H. Schmid, A. Ranft, G. Heppke, R. A. M. Hikmet, and J. Lub, Liq. Cryst. 14, 911-916 (1993).
5H. Kikuchi, M. Yokota, Y. Hisakado, H. Yang, and T. Kajiyama, Nature Materials 1, 64 (2002).
6A. Yoshizawa, M. Sato, and J. Rokunohe, J. Mater. Chem. 15, 3285-3290 (2005).
7H. J. Coles and M. N. Pivnenko, Nature 436, 997-1000 (2005).
8Y. Hisakado, H. Kikuchi, and T. Nagamura, Adv. Mater. 17, 96 (2005).
9Y. Haseba, H. Kikuchi, and T. Nagamura, Adv. Mater. 17, 2311-2315 (2005).
10S-W. Choi, S. Yamamoto, Y. Haseba, H. Higuchi, and H. Kikuchi, Appl., Phys. Lett. 92, 043119 (2008). •
Hirotsugu Kikuchi is with the Institute for Materials Chemistry and Engineering, Kyushu University, in Fukuoka, Japan. He can be reached at kikuchi@cm.kyushu-u.ac.jp.