Image Enhancements in the Wavelet Domain
Conventionally, consumer electronics has provided a way for the user to adjust the brightness, contrast, hue, saturation, and sharpness of a display. These types of image enhancements can be applied in the image domain after decoding a compressed digital video stream. This article describes a method to perform these enhancements efficiently in the wavelet domain. The result is fewer operations per pixel and, therefore, a more power-efficient solution.
by Barry E. Mapen
CONSUMER ELECTRONICS typically provides the user with the option to adjust the basic picture quality on their displays by tweaking the brightness, contrast, hue, saturation, and sharpness. One method of doing this is to adjust the value of each pixel just before the image is sent to the display. This involves scaling (multiplication) and offsetting (addition) each pixel by the adjustment values. Because this operation is performed directly on the image that is displayed, it is considered an image-domain or spatial-domain algorithm. Alternately, the same enhancements can be achieved using fewer operations on the compressed image in the frequency domain and, more specifically, the wavelet domain. The result is a reduction in power consumption, which is critical for portable applications. This article provides a brief overview of wavelet-based image compression to understand how an image is mapped in and out of the wavelet domain and describes how to perform the same image enhancements in the wavelet domain.
Compression
Compression algorithms (codecs) seek to represent the original video sequence using fewer bits by removing redundant information. This is accomplished by trading more computational cycles (time) for fewer bits (space). This is generally done as a series of invertible processing stages (Fig. 1). The recovered image after decompression may notbe identical to the original image, but it should look close enough to the original image as observed by an average viewer. This relaxation in accuracy enables lossy codecs, such as MPEG, to achieve very high compression ratios.
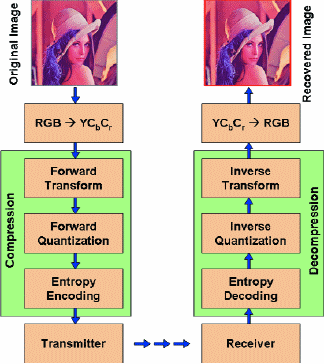
Fig. 1: Generic codec processing flow.
The common compression stages are the transform, quantization, and entropy coding. Additional stages, such as motion compensation, may be implemented to increase the compression ratio, but are not necessary for performing image enhancements in the wavelet domain.
Individual video frames are characterized by the number of pixels used to represent the image, which is more formally known as the spatial resolution. Pixels are characterized by the number of colors they can represent, which is known as the color depth or spectral resolution. How long a frame is presented before changing to the next frame is the frame rate or temporal resolution. The higher the resolution in any dimension (spatial, spectral, or temporal), the more bits are needed to represent the video sequence. This leads to an explosion of data as cameras and information-display devices increase in all three dimensions every year.
To better appreciate this, consider the number of pixels displayed to a user during the course of an average movie. Most standard-definition televisions process and display 30 frames per second (fps) with a spatial resolution of 720 x 480 pixels (0.35 Mpixels). Assuming a movie is 2 hours long (7200 sec), then the total number of pixels displayed is 74,649,600,000 (~75 billion). High-definition television (HDTV) has a spatial resolution of 1920 x 1080 (2.07 Mpixels). This causes the number of pixels to increase by more than a factor of 5. Storing these pixels on DVDs or transporting them over networks requires compression to fit in the available space. To understand how the codec locates redundant information, we follow the original image through the processing stages.
Most of us are familiar with the three-channel red-green-blue (RGB) color space, but there are many equivalent color spaces that can represent the same image (Fig. 2). The most commonly used space for compression is YCbCr which uses a luminance channel and two chrominance channels. Because human vision is heavily biased to the black–and-white portion of the image, the chrominance channels may be scaled down without noticeably changing the appearance of the image. This provides an immediate reduction in the total size of the data stream by 50%.
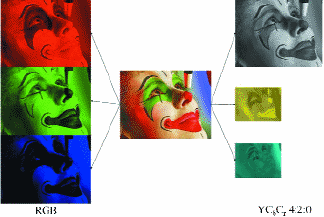
Fig. 2: Equivalent RGB and YCbCr color spaces.

Fig. 3: Calculating details lost by scaling.
Once in the YCbCr color space, each channel is sent to the transform stage where it is converted from the image domain into the wavelet domain. Intuitively, a smaller image takes less space to store than a larger one. It would be great if the transform could simply scale the image down and send a thumbnail to the decoder. Unfortunately, information is lost when scaling down an image. When scaling the image back up to the decoder, the image will look blurry or pixilated. At the encoder, it is possible to scale the image back up, subtract it from the original, and send these details that were lost by scaling to the decoder as shown in Fig. 3.
At the decoder, the small image is scaled back to its original size, and the missing details are added in to fully restore the original image. Wavelets essentially scale the image down and intelligently keep track of the lost details.
The wavelet domain organizes the transformed values into groups by spatial frequency. To visualize the spatial frequencies, consider the image as a 3-D plot where the height of each pixel is its value in that channel. When viewed from directly above, the 3-D plot looks like a normal 2-D image. When viewed from a slight angle, the plateaus and valleys can be seen (Fig. 4). The constant level areas are low spatial frequencies, while the sharp transition areas are high spatial frequencies.
The transform alternately processes the rows and columns of the image by applying high- and low-pass filters (Fig. 5). These filters separate high- and low-frequency areas of the image.
The result is a smaller version of the original image and the three groups that contain the highest horizontal, vertical, and diagonal fre-quencies present in the image. These groups are referred to as sub-bands. This decomposition process is recursively applied on the smaller image (Fig. 6). Most images contain very little high-frequency information, which means most of the coefficients in the sub-band are zeros (black areas). These long runs of zeros can be efficiently represented by the count of zeros between non-zero coefficients, instead of sending over the values for each pixel.

Fig. 4: Visualizing spatial frequencies.
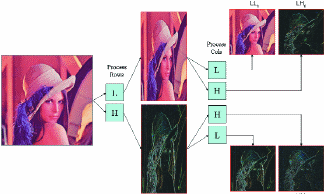
Fig. 5: Wavelet decomposition process.

Fig. 6: Repeated decomposition.
The transform stage is complete when all channels of the image have been transformed (Fig. 7). For more information on wavelet decomposition, see Ref. 1.
The next stage, forward quantization, reduces the variance of coefficients within the band and is the largest source of information loss for most codecs. The simplest quantization technique is the linear algorithm that divides each coefficient by a constant and truncates the result. During decoding, the inverse quantization stage multiplies each coefficient by the same constant. The result is approximately the original value, but may have an error due to the truncation during the forward quantization stage (Fig. 8).
Image Enhancements
There are two key areas of the decoding process where the image-enhancement computations can be performed. The first is during the inverse-quantization stage. Instead of multiplying the coefficients in the sub-band by the same constant used for quantization, we change this constant to a new value that performs one or more of our image enhancements. Similarly, if the enhancement requires changing the value of every pixel in the final image, this can be done by modifying the pixel in the smallest sub-band that resembles the original image (LL0). The change will ripple through the entire image as it is decoded. For reference, the starting images are provided (see Figs. 9 and 10).
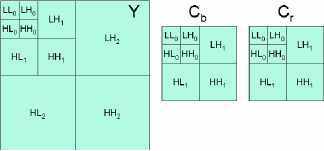
Fig. 7: Complete image decomposition.
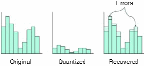
Fig. 8: Linear quantization error.

Fig. 9: Original color.

Fig. 10: Original black and white.

Fig. 11: Adding positive values (+16,384) increases the brightness.

Fig. 12: Adding negative values (–16,384) decreases the brightness.
Brightness
Brightness is a fixed offset added to every pixel in the image domain that causes a shift in the average value (DC level) of the image. Adding positive values increases brightness (Fig. 11) while negative values decreases the brightness (Fig. 12). Typical image domain shifts are in the range of ±31 with a full range of ±255. In the wavelet domain, this energy is mapped to the final approximation (LL0) sub-band in the Y channel (Fig. 13). To change value, offsets can be added to every pixel in this sub-band. The range of the offset is larger than in the image domain and is dependent on the number of levels of decomposition. However, an addition is one operation regardless of the value being added. Since there are far fewer coefficients in the Y-LL0 sub-band than in the final image, this enhancement is more efficient in the wavelet domain. The modified area is shown in red in Fig. 13 to give a relative perspective on the number of points modified.
Contrast
Contrast is a constant multiplier applied to every pixel of each channel in the image domain. To avoid color shifts, the same contrast multiplier must be applied to each channel. Multiplying by values greater than one increases the contrast (Fig. 14) while values less than one decrease the contrast (Fig. 15). Typical contrast multipliers are in the range of 0-1.992. As mentioned earlier, the multiplication must be performed as part of the inverse quantization stage. Changing the value can be done once when the user sets the contrast, resulting in no additional operations while decoding and displaying.
Hue
Looking at a color wheel, hue is generally defined as a rotation of the wheel by an angle. In the YCbCr color space, this equates to
Cb ¢ = Cbcos(θ) + Crsin(θ),
Cr ¢ = Crcos(θ) + Cbsin(θ).
Positive angles produce a rotation toward blue (Fig. 16) while negative angles produce a rotation towards yellow (Fig. 17). Typical hue angles are in the range of ±30°. Hue is applied equally to the entire image, and thus the infor-mation is stored in the Cb-LL0 and Cr-LL0 sub-bands of the chrominance channels. To change the hue, compute the coefficients in Cb-LL0 and Cr-LL0 by the formula above. The cosine and sine of the requested angle may be computed once during set-up and used as a fixed percentage in subsequent computations. This operation is not free, but follows the same efficiency argument as brightness adjustments in the wavelet domain (Fig. 18).

Fig. 13: Brightness adjustment map.

Fig. 14: Multiplying by values greater than than one (1.5x) increases the contrast.

Fig. 15: Multiplying by values less than one (0.5x) decreases the contrast.

Fig. 16: Positive angles (+10°) produce a rotation towards blue.

Fig. 17: Negative angles (–10°) produce a rotation towards yellow.
Saturation
Saturation is a constant multiplier applied only to the chrominance channels in the image domain. Multiplying by values greater than one increases the saturation (Fig. 19) while values less than one decrease the saturation (Fig. 20). As with contrast, saturation multipliers are in the range of 0–1.992.
In the wavelet domain, this equates to applying the multipliers to the Cb-LL0 and Cr-LL0 sub-bands. Similar to contrast, this can be done as a free operation by modifying the inverse quantization constant.
Sharpness
Sharpness is perceived by increasing the amplitude of high-frequency luminance information in an image. Because of this, every sub-band except LL0 in the Y-channel are scaled by a constant. Multiplying by values greater than one increases the sharpness (Fig. 21) while values less than one decrease the sharpness (Fig. 22). Typical sharpness multipliers are in the range of 0–1.992. Because of the hierarchical dependence of the sub-bands on one and other, the same constant must be used across each of the sub-bands (Fig. 23).
Results
The goal of this work is to provide more efficient methods of image-enhancement images from compressed data streams. Assuming the stream must be decoded, the comparison is between decoding and then applying the enhancement verses applying the enhancement in the wavelet domain. Table 1 summarizes the additional operations per pixel ignoring any one-time initialization operations. The fractional results are based on the number of coefficients in the LL0 sub-band that is dependent on the number of times the decomposition process is recursively applied (γ). Simply put, these values will always be less than one. Considering how many pixels must be processed per second, the additional operations for traditional processing quickly add up.
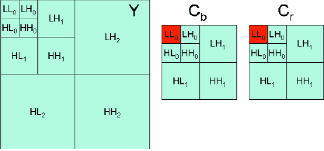
Fig. 18: Hue adjustment map.
Fig. 19: Multiplying by values greater than one (1.5x) increases the saturation.

Fig. 20: Multiplying by values less than one (0.5x) decreases the saturation.

Fig. 21: Multiplying by values greater than one (1.5x) increases the sharpness.

Fig. 22: Multiplying by values less than one (0.5x) decreases the sharpness.
It should be noted that the traditional counts include the added memory accesses to read and store the results since this is done as an independent pass over the data. Therefore, if combining multiple enhancements, the total cost would be less than the sum of those operations. For example, brightness and contrast can be implemented in a single pass requiring only one load and one store.
Conventionally, these processing steps are performed on the video image in the analog domain, before digital quantization, and, in this case, no processor power is required. Analog circuits in color TVs and video amplifiers made these adjustments in response to analog controls or knobs adjusted by the user. However, modern video-processing systems increasingly convert the incoming video signals directly to digital values at the very beginning of the processing chain before additional processing is performed, necessitating clever ways to minimize the processing burden and maximize data throughput.
Conclusions
Using the technique described herein, basic image enhancements may be implemented with little or no additional computational loading. The result is a reduction in power consumption compared with conventional decoding and then enhancing.
It should also be noted that this work can be applied to other transforms including the discrete cosine transform (DCT) used by MPEG. For a more thorough discussion of these and other enhancements in the image domain see Ref. 2, and for the equivalent enhancements in the wavelet domain see Ref. 3.
In addition, using this technique makes it possible to independently adjust multiple streams when decoding, which may be desirable for applications such as security where multiple cameras are displayed on a single monitor. Here, the image enhancements are compensating more for variations of the cameras than variations of the display.
References
1S. G. Mallat, "A theory for multiresolution signal decomposition: The wavelet representation," IEEE Trans. Patt. Anal. Mach. Intell.11(7), 674–693 (1989).
2J. Keith, Video Demystified: A Handbook for the Digital Engineer, third edition (LLH Technology Publishing, Virginia, 2001).
3B. E. Mapen, "White Paper on Integrated Wavelet Decoding Image Enhancements," Anteon/SEG Engineering Technology Center,Control No. ETC:RPT:102493/-(U) (2004). •
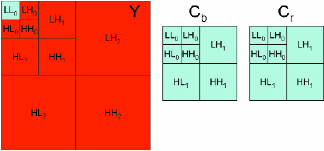
Fig. 23: Sharpness adjustment map.
Table 1: Additional operations per pixel.
|
Enhancement
|
Wavelet Domain
|
Traditional
|
|
Brightness
|
|
5
|
|
Contrast
|
0
|
5
|
|
Hue
|
|
9
|
|
Saturation
|
0
|
5
|
|
Sharpness
|
0
|
22
|
Barry E. Mapen is with Alion, 240 Oral School Rd., Mystic, CT 06355; telephone 860/415-2282, e-mail: Barry.Mapen@gmail.com