Diffusion Confusion

by Edward F. Kelley
There seems to be some confusion in the display industry regarding the use of the term "diffuse" as applied to reflection. Strictly speaking, diffuse reflection means to scatter out of the specular or regular geometrical direction, whereas the term specular or regular reflection refers to reflection as from a perfect mirror, without any diffusion or scattering (see definitions box). If a display has a specular component of reflection, then we will be able to see distinct virtual images of the sources in the room as we gaze at the surface reflections from the display. When other types of reflection properties are present, such as a background gray or a fuzzy smearing of the light sources, then we have diffuse reflection properties. Unfortunately, many people confuse the term "diffuse" with "Lambertian," which is not correct. Lambertian refers to a special type of diffusion, but diffusion is not limited to Lambertian surfaces.
Some refer to a Lambertian surface as a uniform diffuser. Such a surface obeys Lambert's law: I = I0cosθ, where I is the luminous intensity, I0 is the luminous intensity in the normal direction, and θ is the angle from the normal. This gives rise to the familiar Lambertian characteristic that the luminance L of a Lambertian surface does not change with the direction of observation and that the luminance does not depend upon the direction of the illumination; only the magnitude of the illuminance E is important: L = ρE/π, where ρ is the diffuse reflectance of the material. For a diffuse reflectance of ρ = 1, we have a perfect reflecting diffuser. The white diffuse reflectance standards – white pucks – that are often used are close to being perfect reflecting diffusers, but they are not perfect; they are not perfectly Lambertian.There are many diffuse surfaces in our environment. Walls painted with matte (or flat), semi-gloss, satin, or eggshell paints are all examples of diffuse surfaces that are not Lambertian and for which the equation L = ρE/π is not strictly valid where ρ is assumed to be a constant. Matte wall paints appear Lambertian to the eye, but they are not perfectly Lambertian if we measure them carefully. Unfortunately, many people apply this Lambertian equation to our display surfaces with impunity, without regard to the true nature of the optical diffusion when present, and this can lead to serious errors in reproducibility when comparing the reflection properties of displays from laboratory to laboratory. This is not to say that the equation L = ρE/π cannot be used; we just need to realize that for most materials the ratio L/E is not very constant but depends strongly upon the geometry of the illumination and detector. We cannot use ρ = 0.99, or whatever, for those white pucks for just any source-detector geometry we choose.>
In Fig. 1, we show a laser pointer hitting a flat-panel display (FPD). The FPD reflects the laser light onto a white card in a dark room. The display is assumed to have several reflection properties: specular, producing the bright spot at the center of the card; and haze, a non-Lambertian property that produces the fuzzy ball of light surrounding the bright specular dot. The specular component is represented by the bright line. The haze component is represented by the lobed structure indicative of the luminous-intensity distribution surrounding the specular ray. If the FPD also had a Lambertian component, then there would be a dull-red background covering the white card that would be much dimmer than the haze fuzzy ball. Such a Lambertian component is represented by a spherical distribution in the luminous intensity (the dashed line in Fig. 1).
Anti-glare surfaces arise from a micro-structure on the surface that scatters light away from the specular direction and produces the haze property. These anti-glare surface treatments are often made strong enough that no readily observable specular ray exists; i.e., for such a display there would be no distinct virtual image of the source visible in the display reflections – no bright dot from the laser, just a bright fuzzy ball. This is often very desirable for computer monitors so that lighting in the office does not objectionably interfere with the use of the display. However, the presence of haze makes the measurement of the reflection very difficult, and the measurement result becomes very sensitive to the geometry of the apparatus – both the detector and especially the source geometrical configuration.
How bad can it get? How far off the Lambertian assumption leads us depends upon how accurate we want to be and the geometry of the source and detector. If we want 1% results, a Lambertian assumption is not valid for almost any material under directional lighting (even the white pucks!). If we want 5%, things relax a little, but not by much. Even the white pucks deviate 5% or more from Lambertian, depending upon the direction of the illumination. What about anti-glare treatments? We should never use the Lambertian assumption! That is, when we make a Lambertian assumption, what we generally mean is that we measure a reflectance factor R =πL/E in some source/detector geometry and then use that reflectance factor R for other different geometries. Nope, in general, we cannot do such a thing with accuracy, especially whenever haze is present and non-trivial.
How far off we will be on any of these materials depends upon the nature of the bi-directional reflectance distribution function (BRDF) of the material. The BRDF in its simplest expression is the ratio of luminance to illuminance: B = L/E (kids, don't use this at home; the BRDF is usually taken with very well-defined sources and not just a light source placed at an angle). We can use these BRDFs to estimate what might happen to our measurement results if we looked at the display from the normal direction and moved a small light source off to the right as a function of angle. For Lambertian materials, the BRDF is flat. That would mean that the ratio of the luminance to illuminance is constant, independent of the angle of the source from the normal. In Fig. 2, we show a BRDF of a plasma-display panel (PDP) in blue and a liquid-crystal display (LCD) in red on a linear scale; here, the background gray of the PDP will look like dark-gray matte wall paint to our eyes. Rather than having a flat BRDF as a Lambertian material would, the PDP BRDF fall-off is approximately 2% per degree from a source angle of 20–80° and approximately 1% per degree at a source angle of 30°. To the eye, such a BRDF would appear to be flat and Lambertian, but not to our instruments.
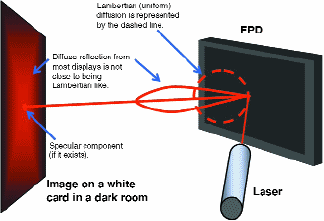
Fig. 1: Visualizing the planar projection of the BRDF.
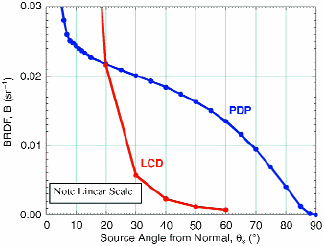
Fig. 2: Comparison of PDP and LCD BRDFs on a linear scale.
Figure 3 shows the BRDFs of both displays on a log scale. The LCD has an anti-glare front surface with no specular component. The PDP has glass front surfaces with an anti-reflection coating (not an anti-glare micro-structure) to reduce reflections. The glass produces a specular component (resembling a delta function) at a 0° source angle – the specular or mirror direction. This rendering on a log scale is approximately how the eye sees things, and the PDP appears to be very Lambertian away from the specular, but only to the eye. For the LCD, the BRDF is changing about 10% per degree or more around 30°.
How sensitive the measurement results are depends upon the geometrical configuration of the source and detector. If we apply a uniform diffuse illumination and measure the reflected luminance from off the normal by 6–10°, we will obtain a result that is very reproducible – a diffuse-reflectance measurement. The material is not Lambertian by any means, but the apparatus yields very reproducible results. The measurement result, the reflectance factor R = πL/E (or diffuse reflectance ρ), cannot be used for other geometries of source and detector except for this uniform-diffuse-illumination source with the detector off normal from about 5–12°.
If we arrange a light source at some angle away from the normal and measure the luminance of the surface from the normal, the resulting luminance will vary considerably, depending upon the angle of the source as shown by the BRDFs above. For a PDP, if we have a source at, for example 30°, then we will obtain almost the same ratio L/E if we were to increase the diameter of the source quite a bit. Within 5% or so, the same may be true for an LCD. But if we change the angle of the source 2° toward the normal, the luminance of the PDP may measure almost the same, within 5%, but the luminance of the LCD will measure quite differently, an increase of 20% or more.
We can always write L = πE/R for any geometry of source and detector, but that geometry must be carefully specified. However, the reflectance factor R (or diffuse reflectance ρ, or luminance factor ß) is only a constant for Lambertian materials, of which there are none. The reflectance factor R is sensitive to the geometry of the apparatus. The smaller the source, the more sensitive R can be to geometry in general. Because of this confusion of diffusion and Lambertian properties, some say we have "diffuse illumination" when we place a discrete source at some angle away from the normal and view the screen from the normal, and then they apply the Lambertian assumption. If the material were Lambertian, then the reflectance factor measured this way would be the same as the diffuse reflectance measured in an integrating sphere. A better term to describe the illumination from such an isolated source is "directed-source illumination." Such a term clearly distinguishes the illumination from a more uniform diffuse illumination. This may help avoid the historical temptation to apply Lambertian models to all light-diffusing materials.
|
Reference: CIE Publication No. 17.4, International Lighting Vocabulary, Commission Internationale de l'Eclairage (International Commission on Illumination), 1987. A joint publication with the International Electrotechical Commission: IEC Publication 50(845), International Electrotechnical Vocabulary, Chapter 845: Lighting, 1987.
CIE 17.4: 845-04-45 "regular reflection; specular reflection.
Reflection in accordance with the laws of geometrical optics, without diffusion."
CIE 17.4: 845-04-44 "diffusion; scattering.
Process by which the spatial distribution of a beam of radiation is changed when it is deviated in many directions by a surface or by a medium, without change of frequency of its monochromatic components."
'Note — A distinction is made between selective diffusion and non-selective diffusion according to whether or not the diffusing properties vary with the wavelength of the incident radiation.'
CIE 17.4: 845-04-54 "perfect reflecting diffuser.
Ideal isotropic diffuser with a reflectance equal to 1."
CIE 17.4: 845-04-58 "reflectance (for incident radiation of given spectral composition, polarization and geometrical distribution) (r) unit: 1.
Ratio of the reflected radiant or luminous flux to the incident flux in the given conditions."
|
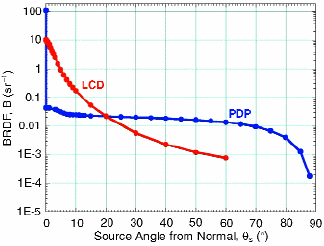
Fig. 3: Comparison of LCD and PDP BRDFs on a log scale.
Whenever complicated reflection properties such as haze exist with our displays, we no longer should employ the simplified equation that is used for Lambertian materials. Whereas haze is a form of diffuse reflection, it is not Lambertian. It is fine to think in terms of diffusion when considering reflection, but diffusion does not automatically mean Lambertian. •
Edward F. Kelley works in the Optoelectronics Division, Electronics and Electrical Engineering Laboratory, U.S. Department of Commerce, NIST, Boulder, CO; e-mail: kelley@nist.gov.
This is a contribution of the National Institute of Standards and Technology and is not subject to copyright.