|
The Spatial Standard Observer: A new tool for display metrology
In the design of displays, "beauty is in the eye of the beholder." But until recently, the industry has lacked tools to estimate quality as seen by the human eye. Here, the development and application of the Spatial Standard Observer (SSO), a new tool for estimating the visibility of spatial patterns, is detailed. Similar to measurements of luminance, or of CIE color coordinates, the SSO provides another means of measuring displays in units that are meaningful to the human observer.
by Andrew B. Watson
WE ARE in a time of explosive growth in digital display technologies, applications, and markets. During design and manufacture, displays are measured with instruments to quantify their visual quality. For this purpose, it would be useful to have an instrument that could mimic the performance of the human observer. We have developed an instrument of this kind – the Spatial Standard Observer (SSO), a software algorithm that incorporates a simple model of human-visual sensitivity to spatial contrast for use in a wide variety of display inspection and measurement applications.
The SSO began in an effort to account for the results of a research project known as ModelFest. This was a collaboration among an international consortium of vision-research groups, who sought to create a common set of benchmark data to describe human sensitivity to spatial patterns.1-3 They designed a set of 43 standard stimuli, and collected contrast thresholds for each stimulus from a total of 16 human observers. A contrast threshold is a measure of the smallest amount of contrast that is required for the image to be visible. Contrast is the variation on luminance in the image, expressed as a fraction of the average luminance. The data showed large variations (about 1.5 log units) among the different spa-
Andrew B. Watson is the Senior Scientist for Vision Research at the NASA Ames Research Center, MS 262-2, Moffett Field, CA 94035-1000; telephone 650/604-5419, fax -3323, e-mail: andrew.b. watson@nasa.gov.
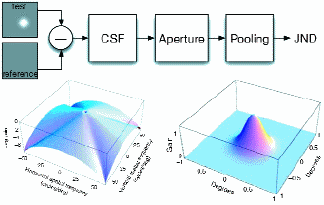
Fig. 1: Overview of the Spatial Standard Observer. The difference between test and reference images is filtered by a contrast-sensitivity function (CSF), windowed by an aperture function, and pooled non-linearly over space. The two graphs show the CSF (left) and the aperture (right).
tial patterns. Following collection of the data, the theoretical challenge was to account for these variations with a model of visual spatial processing. In our lab, we found that the data could be accounted for with a rather simple model.2,3 That model formed the basis for the SSO, which is outlined in Fig. 1.
|

Fig. 2: Example of SSO mura measurement. The left image is a capture of a 17-in. LCD panel. The right image shows the SSO output image, thresholded at 2 JND. The peak value is 4.1 JND.
|
The input to the model is a pair of images: test and reference. The difference between test and reference images is filtered by a contrast-sensitivity function (CSF). The CSF is a measure of the visibility of different spatial frequencies at different orientations. Spatial frequencies are sinusoidal variations in contrast over space. This function is two-dimensional and reflects the decline in human-visual sensitivity at higher spatial frequencies and at very low frequencies, as well as the lower sensitivity at oblique orientations (the oblique effect).
The filtered image is then multiplied by an aperture function. This reflects the decline in human-visual sensitivity with distance from the point of fixation. The final step is to pool the resulting image over space, using a non-linear Minkowski metric, in which the absolute value of each pixel is raised to a power beta, summed, and then the beta root is taken. Beta is a parameter of the model, which here has a value of about 2.4. Because the SSO metric is calibrated against a large corpus of human data, the output is in units of just-noticeable difference (JND). This means that if two images differ by 1 JND, they should be just discriminable.
The SSO operates on digital images that subtend 2° or less, viewed from a specific distance, and whose pixels have a known relation to luminance. Extensions of the basic metric incorporate spatial masking, viewing of larger images, and color.
Mura Inspection
While flat-panel-display manufacturing is highly automated, most flat panels are examined for defects by human inspectors. This inspection stage is slow and costly, and becomes more difficult as panel sizes increase. Reliability and consistency of inspection are also generally unknown.
One important category of defect is called "mura," derived from the Japanese word for blemish.4 Mura are typically low-contrast spots, smudges, and streaks of various shapes and sizes that are visible when the display is driven at a uniform value. Different types of mura arise through different defects in the structure of the display. There have been previous efforts to define and quantify mura.4,5 However, these definitions do not provide a clear method for measuring real mura, in part because the definitions are normative and do not provide general measurement methods.
To automate the process of display inspection, it is necessary to compute the visibility of the defect to a human. This requires a calibrated model of human sensitivity to spatial patterns such as the SSO.
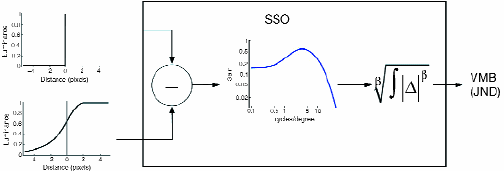
Fig. 3: Motion-blur metric based on the Spatial Standard Observer. An ideal edge and the motion-blurred edge are subtracted and the difference is filtered by a contrast-sensitivity function and pooled nonlinearly over space. The result is a visible motion-blur measure (VMB) in units of JND.
To apply the SSO to mura detection, a single image of the display under test is acquired. This image is first preprocessed to remove signals that are not of interest. It may also be cropped and down-sampled. A reference image is then created from this image by removing mura-like signals. Test and reference images are then compared and their difference measured. The SSO produces measurements in units of JND. In a typical mode of operation, the SSO produces both an image showing the location of the mura, as well as a peak JND measure, defining the worst artifact in the image.
|